In my previous post, I walked through the creation of a simple binary search tree in JavaScript. That post discussed adding nodes into the tree and traversing the tree to location and extra information. The one major piece missing to the discussion was removing of nodes from a binary search tree. Removing nodes from a binary search tree can be complex because the tree must remain balanced, with all values on the left being less than all the values on the right.
When removing a node, you’ll need to determine if it’s the root node. Root nodes are handled similarly to others with the obvious exception that the root node will need to be set to a different value at the end. To make things easy, this will be considered a special case in the JavaScript code.
The first step to removing a node is to determine whether or not the node actually exists:
BinarySearchTree.prototype = {
//more code here
remove: function(value){
var found = false,
parent = null,
current = this._root,
childCount,
replacement,
replacementParent;
//make sure there's a node to search
while(!found && current){
//if the value is less than the current node's, go left
if (value < current.value){
parent = current;
current = current.left;
//if the value is greater than the current node's, go right
} else if (value > current.value){
parent = current;
current = current.right;
//values are equal, found it!
} else {
found = true;
}
}
//only proceed if the node was found
if (found){
//continue
}
},
//more code here
};The first part of the remove() method is to locate the node to remove using a binary search, going left if the value is less than the current node or right if it’s greater. As this traversal occurs, the parent node is also tracked because you’ll ultimately need to remove the node from its parent. When found is equal to true, the value of current is the node to remove.
There are three conditions to worry about when removing a node:
- A leaf node
- A node with just one child
- A node with two children
Removing anything but a leaf node from a binary search tree means that values must be moved around to properly order the tree. The first two are relatively simple to implement, a leaf node is simply removed and a node with one child is removed and replaced with its child. The last case is a bit complex, so that will be visited later.
Before knowing how to remove the node, you’ll need to know how many children exist on the node. Once that is known, you must determine if the node is the root, leaving a fairly straightforward decision tree:
BinarySearchTree.prototype = {
//more code here
remove: function(value){
var found = false,
parent = null,
current = this._root,
childCount,
replacement,
replacementParent;
//find the node (removed for space)
//only proceed if the node was found
if (found){
//figure out how many children
childCount = (current.left !== null ? 1 : 0) +
(current.right !== null ? 1 : 0);
//special case: the value is at the root
if (current === this._root){
switch(childCount){
//no children, just erase the root
case 0:
this._root = null;
break;
//one child, use one as the root
case 1:
this._root = (current.right === null ?
current.left : current.right);
break;
//two children, little work to do
case 2:
//TODO
//no default
}
//non-root values
} else {
switch (childCount){
//no children, just remove it from the parent
case 0:
//if the current value is less than its
//parent's, null out the left pointer
if (current.value < parent.value){
parent.left = null;
//if the current value is greater than its
//parent's, null out the right pointer
} else {
parent.right = null;
}
break;
//one child, just reassign to parent
case 1:
//if the current value is less than its
//parent's, reset the left pointer
if (current.value < parent.value){
parent.left = (current.left === null ?
current.right : current.left);
//if the current value is greater than its
//parent's, reset the right pointer
} else {
parent.right = (current.left === null ?
current.right : current.left);
}
break;
//two children, a bit more complicated
case 2:
//TODO
//no default
}
}
}
},
//more code here
};When dealing with the root, it’s a simple process of overwriting it. For non-root nodes, the appropriate pointer on the parent must be set based on the value of the node to remove: if the removed value was less than the parent, then the left pointer must be reset either to null (for nodes with no children) or removed node’s left pointer; if the removed value was greater than the parent, then the right pointer must be reset either to null or the removed node’s right pointer.
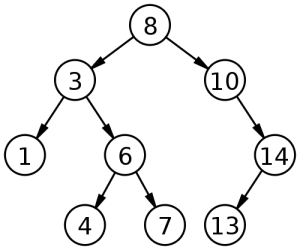
Removing a node with two children, as mentioned previously, is the most complex operation. Consider the following representation of a binary search tree.
With a root of 8 and a left child of 3, what would happen if the 3 was removed? There are two possibilities: 1 (3′s left child, called the in-order predecessor) could take the place of 3 or 4 (the left-most child of the right subtree, called the in-order successor) can take the place of 3.
Either of these two options is appropriate. To find the in-order predecessor, the value that comes before the value being removed, examine the left subtree of the node to remove and select the right-most descendant; to find the in-order successor, the value that comes immediately after the value being removed, reverse the process and examine the right subtree for the left-most descendant. Each of these requires another traversal of the tree to complete the operation:
BinarySearchTree.prototype = {
//more code here
remove: function(value){
var found = false,
parent = null,
current = this._root,
childCount,
replacement,
replacementParent;
//find the node (removed for space)
//only proceed if the node was found
if (found){
//figure out how many children
childCount = (current.left !== null ? 1 : 0) +
(current.right !== null ? 1 : 0);
//special case: the value is at the root
if (current === this._root){
switch(childCount){
//other cases removed to save space
//two children, little work to do
case 2:
//new root will be the old root's left child
//...maybe
replacement = this._root.left;
//find the right-most leaf node to be
//the real new root
while (replacement.right !== null){
replacementParent = replacement;
replacement = replacement.right;
}
//it's not the first node on the left
if (replacementParent !== null){
//remove the new root from it's
//previous position
replacementParent.right = replacement.left;
//give the new root all of the old
//root's children
replacement.right = this._root.right;
replacement.left = this._root.left;
} else {
//just assign the children
replacement.right = this._root.right;
}
//officially assign new root
this._root = replacement;
//no default
}
//non-root values
} else {
switch (childCount){
//other cases removed to save space
//two children, a bit more complicated
case 2:
//reset pointers for new traversal
replacement = current.left;
replacementParent = current;
//find the right-most node
while(replacement.right !== null){
replacementParent = replacement;
replacement = replacement.right;
}
replacementParent.right = replacement.left;
//assign children to the replacement
replacement.right = current.right;
replacement.left = current.left;
//place the replacement in the right spot
if (current.value < parent.value){
parent.left = replacement;
} else {
parent.right = replacement;
}
//no default
}
}
}
},
//more code here
};The code for both the root and non-root removal of nodes with two children are almost the same. This implementation always looks for the in-order predecessor by looking to the left subtree and finding the right-most descendant node. The traversal is done using the replacement and replacementParent variables in a while loop. The node in replacement ends up being the node to replace current, so it’s removed from its current location by setting its parent’s right pointer to the replacement’s left pointer. In the case of the root node, replacementParent will be null when the replacement is an immediate child of the root node, so the replacement‘s right pointer is just set to the root’s right pointer. The last step is to assign the replacement node into the correct location. For the root node, the replacement is set to be the new root; for non-root nodes, the replacement is assigned to the appropriate location on the original parent.
A note about this implementation: always replacing nodes with the in-order predecessor can lead to an unbalanced tree, wherein most of the values are on one side of the tree. An unbalanced tree means less efficient searches and so are cause for concern in real-world scenarios. There are binary search tree implementations that determine whether to use the in-order predecessor or the in-order successor to keep the tree properly balanced (typically called self-balancing binary search trees).
The full source code for this binary search tree implementation is available at my Computer Science in JavaScript GitHub project. For an alternate implementation, you can also check out Isaac Schlueter‘s GitHub fork.